\(tan^{1}(x) tan^{1}(y) = \pi tan^{1} (\frac{x y}{1 – xy})\) \(2 sin^{1}(x) = sin^{1}(2x\sqrt{1x^{2}})\) \(3sin^{1}(x) = sin^{1}(3x4x^{3})\) \(\sin ^{1}x \sin ^{1}y=\sin ^{1}(x\sqrt{1y^{2}}y\sqrt{1x^{2}}), if x, y \geq 0 and x^{2}y^{2} \leq 1\)Inverse Trigonometric Functions (Simplification and Examples) video tutorial Inverse Trigonometric Functions (Simplification and Examples)The derivative of tan inverse x is given by (tan1 x)' = 1/(1 x 2) The differentiation of tan inverse x is the process of finding the derivative of tan inverse x with respect to x The derivative of tan inverse x can be calculated using the concept of derivatives and inverse trigonometric functions

Prove That Tan Inverse X Tan Inverse 2x 1 X Square Tan Inverse 3x X Cube 1 3x Square X Maths Inverse Trigonometric Functions Meritnation Com
Tan inverse 2x formula
Tan inverse 2x formula- In mathematics, inverse trigonometric functions are also known as arcus functions or antitrigonometric functions The inverse trigonometric functions are the inverse functions of basic trigonometric functions, ie, sine, cosine, tangent, cosecant, secant, and cotangent It is used to find the angles with any trigonometric ratioDerivative of inverse tangent Calculation of Let f (x) = tan 1 x then,
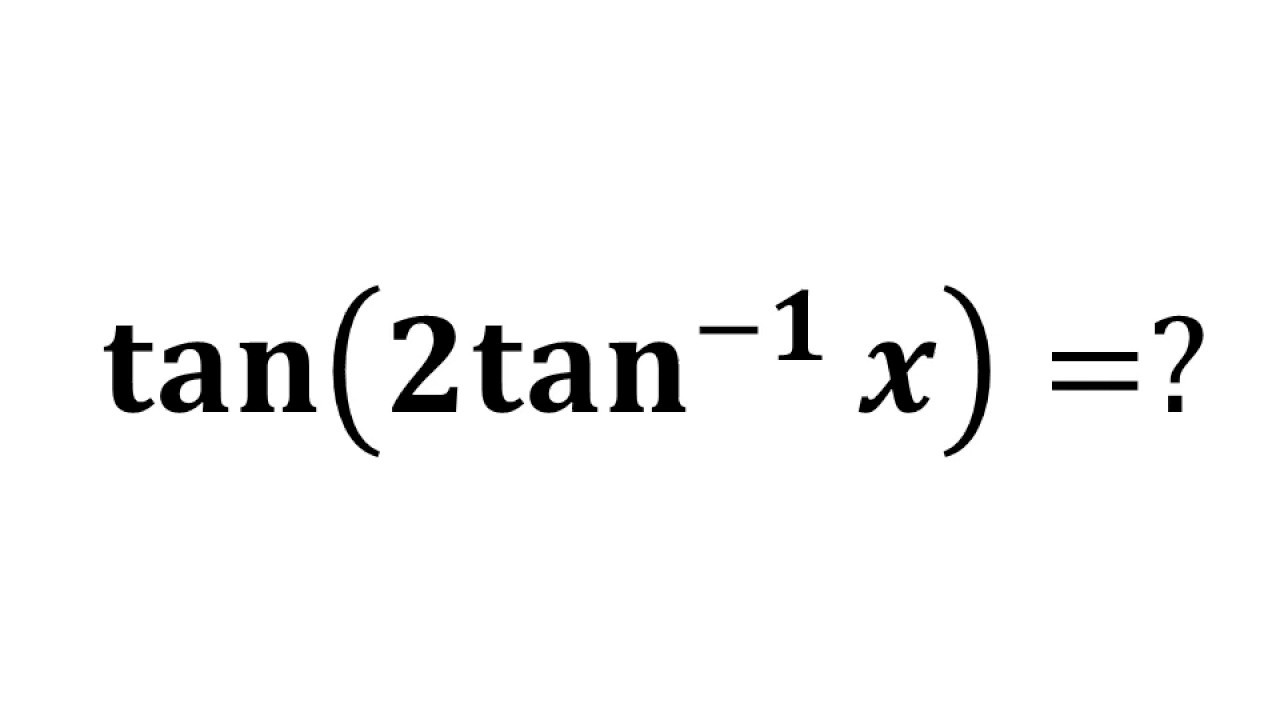



Tan 2 Tan 1 X Tan 2 Arctan X Youtube
We can go directly to the formula for the antiderivative in the rule on integration formulas resulting in inverse trigonometric functions, and then evaluate the definite integral We have ∫1 0 dx √1−x2 =sin−1x1 0 =sin−11−sin−10 = π 2 −0 = π 2 ∫ 0 1 d x 1 − x 2 = sin − 1 Representation of Inverse Trigonometric Functions They are represented by adding arc in prefix or by adding 1 to the power Inverse sine can be written in two ways sin1 x; Solution Let y = tan−12x tany = 2x Differentiating both side with respect to 'x' d dx (tany) = d dx (2x) ⇒ sec2y( dy dx) = 2 ⇒ dy dx = 2 sec2y ⇒ dy dx = 2 1 tan2y
Finding the derivatives of the main inverse trig functions (sine, cosine, tangent) is pretty much the same, but we'll work through them all here just for drill 1 Derivative of sin 1 (x) We're looking for d d x s i n − 1 ( x) If we let y = s i n − 1 ( x) then we can apply f (x) = sin (x) to both sides to get2tan1 x = sin1 (2x/(1x 2)), x ≤ 1;Also, what is the derivative of tan 1 2x?
An inverse tan, also known as a tangent, is the inverse of the tangent function or opposite Since the tangent function normally takes an angle measurementInverse Tangent Calculator There are 2 different ways that you can enter input into our arc tan calculator You can enter input as either a decimal or as the opposite over the adjacent Method 1 Decimal Enter a decimal number Method 2 Opposite / Adjacent Entering the ratio of the opposite side divided by the adjacent Example 13Solve tan–1 2x tan–1 3x = π/4Given tan–1 2x tan 3x = π/4 tan–1 ((2x 3x)/(1 − 2x × 3x)) = π/4 𝟓𝐱/(𝟏 − 𝟔𝐱𝟐) = tan 𝝅/𝟒We know that tan–1 x tan–1 y = tan–1 ((𝐱 𝐲)/(𝟏 − 𝐱𝐲)) Replacing x by 2x & y by 3x 5x/(1− 6x2) = 1 5x = 1 × (1 – 6x2)5x = (टीचू)
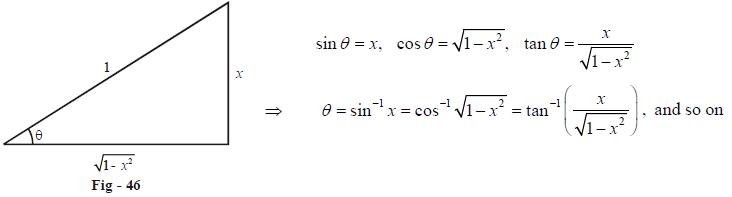



Interconversion Between Inverse Trigonometric Ratios What Is Interconversion Between Inverse Trigonometric Ratios Examples Solutions Cuemath




Ex 5 3 9 Find Dy Dx In Y Sin 1 2x 1 2x2 Chapter 5
52x 79x 16x x 266x 27x cos sin tan acos asin atan atan2 sqrt 1/x log exp fmod cles CPU Cycle Improvement Compiler mathh library MSPMATHLIB Benchmarks wwwticom 21 Performance Figure 1 shows the average CPU cycles needed to calculate a result for the existing MSP430 math implementations and for MSPMATHLIBProportionality constants are written within the image sin θ, cos θ, tan θ, where θ is the common measure of five acute angles In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengthsDerivative of Tangent Inverse In this tutorial we shall explore the derivative of inverse trigonometric functions and we shall prove the derivative of tangent inverse Let the function of the form be y = f ( x) = tan – 1 x By the definition of the inverse trigonometric function, y = tan – 1 x can be written as tan




Ex 2 2 5 Simplify Tan 1 Root 1 X2 1 X Chapter 2



Solve For X Tan 1 X 1 X 1 Tan 1 2x 1 2x 1 Tan 1 23 36 Sarthaks Econnect Largest Online Education Community
The integration of tangent inverse is of the form I = ∫ tan – 1 x d x To solve this integration, it must have at least two functions, however it has only one function tan – 1 x So, consider the second function as 1 Now the integration becomes I = ∫ tan – 1 x ⋅ 1 d x – – – ( i) The first function is tan – 1 x and the tan1 x cot1 x = π/2 , x ∈ R 9 sec1 x cosec1 x = π/2 ,x ≥ 1 10 sin1 (1/x) = cosec1 (x), if x ≥ 1 or x ≤ 1 11 cos1 (1/x) = sec1 (x), if x ≥ 1 or x ≤ 1 12 tan1 (1/x) = cot1 (x), x > 0 13 tan1 x tan1 y = tan1 ((xy)/(1xy)), if the value xy < 1 14 tan1 x – tan1 y = tan1 ((xy)/(1xy)), if the value xy > 1 15In mathematics, the inverse trigonometric functions (occasionally also called arcus functions, antitrigonometric functions or cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted domains)Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of




Cos2x 1 Sin2x Tan Pi 4 X Double And Half Angle Identity Youtube




Inverse Of Tan 35 Images The Graph Of The Inverse Tangent Function Geometry 7 7 Integration Of Inverse X
Thanx for A tan inverse of x give angle as answer tan is positive in 1st and 3rd quadrant Tan is negative in 2nd and 4th quadrant Tan is periodic with 180° tan (180° x) = tan x So in case of tan angle is of real importance till 180° 1for posiAlso, these formulas include the sum and difference of two inverse tangent functions Tan −1(−x) = −Tan −1(x) Tan − 1 ( − x) = − Tan − 1 ( x) Tan −1(x) = Cot −1 1 x Tan − 1 ( x) = Cot − 1 1 x Tan −1(x) Cot −1(x) = π 2 Tan − 1 ( x) Cot − 1 ( x) = π 2 Inverse tan is the inverse function of the trigonometric function 'tangent' It is used to calculate the angle by applying the tangent ratio of the angle, which is the opposite side divided by the adjacent side of the right triangle Based on this function, the value of tan 1 or arctan 1 or tan 10, etc




Ex 2 2 4 Prove 2tan 1 1 2 Tan 1 1 7 Tan 1 31




2tan 1 X Sin 1 2x 1 X 2 2arctan X Arcsin 2x 1 X 2 Youtube
Inverse Function Calculator The calculator will find the inverse of the given function, with steps shown If the function is onetoone, there will be a unique inverse Your input find the inverse of the function $$$ y=\frac {x 7} {3 x 5} $$$(logarithmic, inverse trigonometric, algebraic (usually a power function), trigonometric, or exponential) An exception is integrands of the form Un, where n is a positive integer > 1, and U is a basic trigonometric function such as sin(x) or cos(x) These lead to reduction formulas In this case, peel off one factor as dv and let u = the restThe derivative of the tan inverse function is written in mathematical form in differential calculus as follows ( 1) d d x ( tan − 1 ( x)) ( 2) d d x ( arctan ( x)) The differentiation of the inverse tan function with respect to x is equal to the reciprocal of the




Double Angles Ppt Video Online Download




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube
Tan Inverse Formula The inverse of tan or antitan is the arcus of tan Here, we will define the formula of the tan inverse Suppose we are given as x =tan y then, y =tan1 x Here y can be any real number This is also known as tan inverse x When you add two different tan inverse functions, the formula will be represented as belowGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!The inverse function reverses this operation, taking the ratio of sides as input and returning the angle as output sin − 1 ( b c) = θ cos − 1 ( a c) = θ tan − 1 ( b a) = θ = θ = θ = θ This means the inverse trigonometric functions are useful whenever we
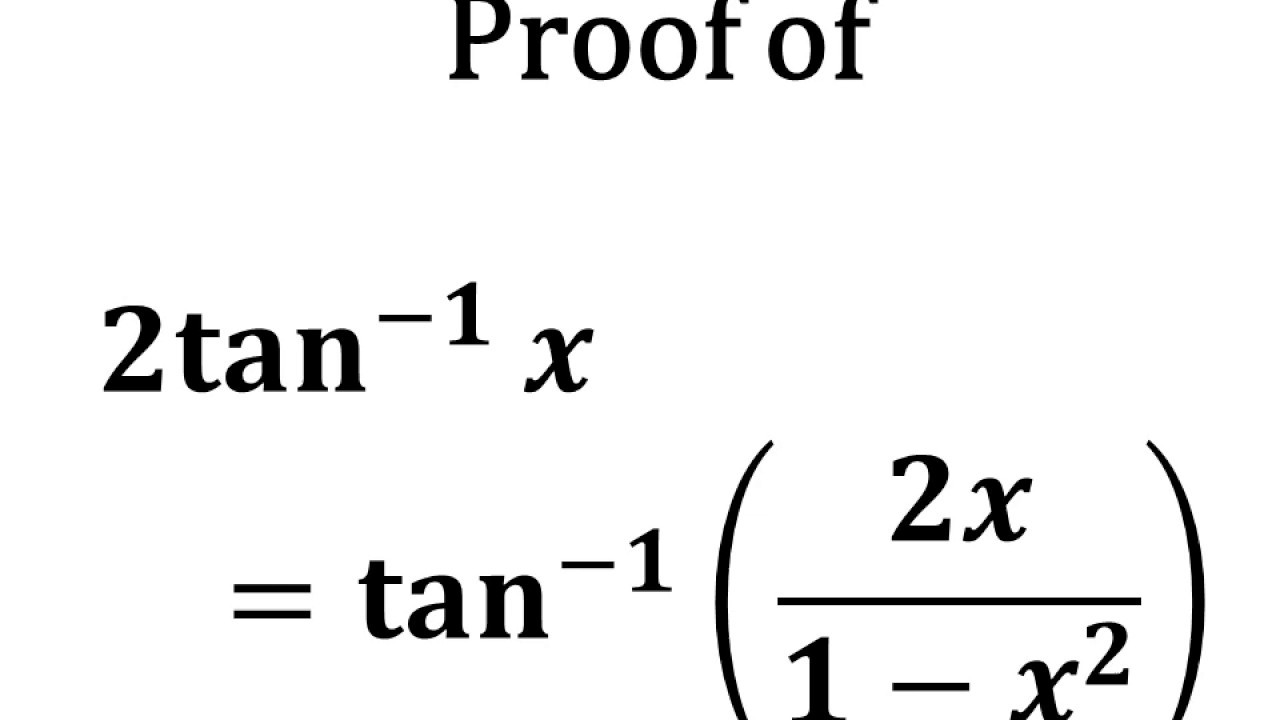



2tan 1 X Tan 1 2x 1 X 2 2arctan X Arctan 2x 1 X 2 Youtube



1
INVERSE TRIGONOMETRIC FUNCTIONS 35 of sine function Thus, the graph of the function y = sin –1 x can be obtained from the graph of y = sin x by interchanging x and y axes The graphs of y = sin x and y = sin–1 x are as given in Fig 21 (i), (ii), (iii)The dark portion of the graph ofTan tangent of a value or expression asin inverse sine (arcsine) of a value or expression acos inverse cosine (arccos) of a value or expression atan inverse tangent (arctangent) of a value or expression sinh Hyperbolic inverse sine (arcsine) of a value or expression cosh Hyperbolic inverse cosine (arccos) of a value or Inverse Tan Formula The following formula is used to calculate the inverse tangent of a value Arctan(x) = C Tan C = X Where C is the angle;



Solve For X Tan 1 X 1 Tan 1 X Tan 1 X 1 Tan 1 3x Sarthaks Econnect Largest Online Education Community




Misc 44 Mcq Value Fo Tan 1 2x 1 1 X X2 Dx Is
Detailed explanation with examples on propertiesofinversetrigonometricfunctions helps you to understand easily , designed as per NCERT QnA , Notes & Videos2tan1 x = cos1 ((1x 2)/(1x 2)), x ≥ 0;Answer and Explanation The derivative of tan1 is 214x2 2 1 4 x 2 Finding the derivative of this function will involve the formula for the derivative of the Also Know, what is the inverse of tangent?



How To Evaluate Tan 2 Tan 1 1 5 Pi By 4 Quora
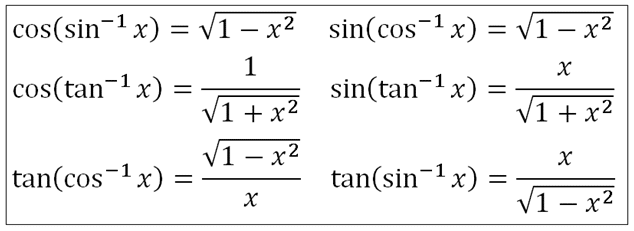



Inverse Trig Identities Reciprocal Of Trigonometric Function Trig
𝑑𝑡/2𝑥 I1 = 1/2 ∫1 1/𝑡 𝑑𝑡 I1 = 1/2 log〖 𝑡〗𝐶1 I1 = 1/2 log〖 1𝑥^2 〗𝐶1 Putting the value of I1 in (1) , ∫1 〖" " tan^(−1) 𝑥" " 〗 𝑑𝑥=𝑥 tan^(−1) 𝑥−∫1 𝑥/(1 𝑥^2 )Tangent calculator Arctangent definition The arctangent function is the inverse function of y = tan(x) arctan(y) = tan1 (y) = x kπ For every k = {,2,1,0,1,2,} For example, If the tangent of 45° is 1 tan(45°) = 1 Then the arctangent of 1 is 45° arctan(1) = tan1 (1) = 45° Arctangent table 3 Derivatives of the Inverse Trigonometric Functions by M Bourne Recall from when we first met inverse trigonometric functions " sin1 x" means "find the angle whose sine equals x" Example 1 If x = sin1 025 then by using the calculator, x = 15° We have found the angle whose sine is 025




Inverse Trigonometric Functions Xii 1




Prove That 2tan 1x Tan 1 2x 1 X 2 Maths Inverse Trigonometric Functions Meritnation Com
Derivatives of inverse trigonometric functions sin1 (2x), cos1 (x^2), tan1 (x/2) sec1 (1x^2)Inverse Trigonometric Functions •The domains of the trigonometric functions are restricted so that they become onetoone and their inverse can be determined •Since the definition of an inverse function says that f 1(x)=y => f(y)=x We have the inverse sine function, sin 1x=y π=> sin y=x and π/ 2Before reading this, make sure you are familiar with inverse trigonometric functions The following inverse trigonometric identities give an angle in different ratios Before the more complicated identities come some seemingly obvious ones Be observant of the conditions the identities call for Now for the more complicated identities These come handy very often, and can easily be




Solved Prove The Identity 3 Tan 3x 9 Tan X 3 Tanx 13 Chegg Com




Misc 44 Mcq Value Fo Tan 1 2x 1 1 X X2 Dx Is
Its inverse trigonometric function It can be shown that the graph of an inverse function can be obtained from the corresponding graph of original function as a mirror image (ie, reflection) along the line y = x 213 Properties of inverse trigonometric functions 1 sin–1 (sin x) = x –, 2 2 x ∈ cos–1(cos x) = x x ∈0, tan–1Arctan The arctan function is the inverse of the tangent function Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Math Backup Posts Facebook




Half Angle Identity Manipulation Mathematics Stack Exchange
X is the tan C;Free online tangent calculator tan(x) calculator This website uses cookies to improve your experience, analyze traffic and display adsTo calculate the value of the tan inverse of infinity (∞), we have to check the trigonometry table From the table we know, the tangent of angle π/2 or 90° is equal to infinity, ie, tan 90° = ∞ or tan π/2 = ∞ Therefore, tan 1 (∞) = π/2 or tan 1 (∞) = 90°




Differentiate Tan 1 2x 1 X 2 W R T Sin 1 2x 1 X 2



What Is Tan Inverse Of 2 Quora
Trigonometric Equation Calculator \square! Solution Let x = sec θ, then x 2 − 1 = s e c 2 θ − 1 = tan θ Therefore, cot–1= 1 x 2 – 1 = cot–1 (cot θ) = θ = sec–1 x, which is the simplest form Inverse trigonometric formula here deals with all the essential trigonometric inverse function which will make it easy for you to learn anywhere and anytime ITF formula for classInverse\f (x)=\ln (x5) inverse\f (x)=\frac {1} {x^2} inverse\y=\frac {x} {x^26x8} inverse\f (x)=\sqrt {x3} inverse\f (x)=\cos (2x5) inverse\f (x)=\sin (3x)




Inverse Trigonometric Functions Trigo Some Important Substitutions Type Put Formula 2x X Sin Cedil Sin2 Cedil 3x 4x3




Derivative Of Tan Inverse With Chain Rule Youtube
What is the inverse tangent?2tan1 x = tan1 (2x/(1 – x 2)), 1 < x Solve the following equations for x tan^1((x 2)/(x 1)) tan^1((x 2)/(x 1)) = π/4 askedApr 2in Trigonometryby Takshii(350kpoints) inverse trigonometric functions class12 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries
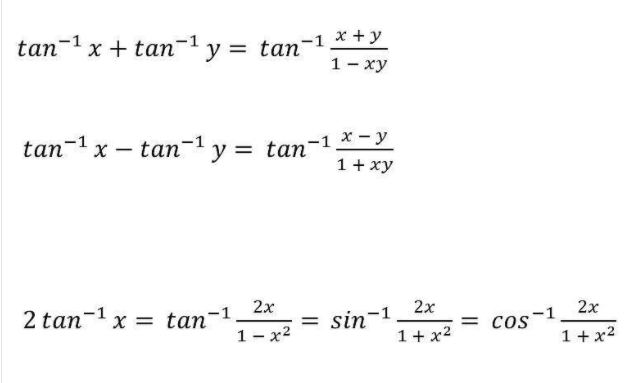



Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec
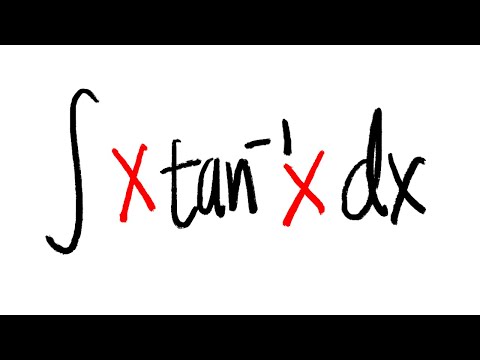



Integral Of X Tan 1 X Youtube
Arcsin x Same goes for cos and tan Note Don't confuse sin1 x with (sin x)1 They are different Writing sin1 x is a way to write inverse sine whereas (sin x)1




Derivative Of Tan Inverse X Formula What Is Derivative Of Arctan




Solved 8 Find The Formula For Sin 2 Tan 1 X A 1 Root 1 Chegg Com



Derivative Of Arctan X Inverse Tangent Detailed Lesson
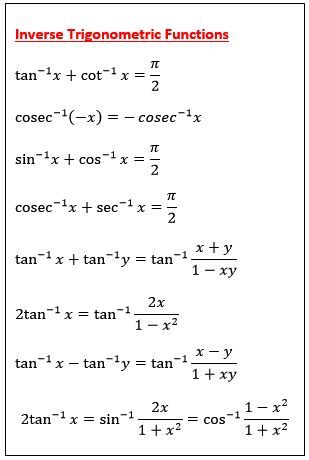



Trigonometry Inverse Formula List Mathematics




Weierstrass Substitution Wikipedia



1




Solve Tan 1 2x Tan 1 3x Pi 4 Youtube




How To Find The Inverse Of A Trig Function Dummies



What Is Cos Tan 1 X Quora




Second Derivative Of Tan 2x Youtube




Solve Tan 1 1 1 2x Tan 1 1 1 4x Tan 1 2 X 2




Example 7 Show That Tan 1 X Tan 1 2x 1 X2 Inverse




Inverse Trigonometric Functions Xii 1




Integrals Of Inverse Trigonometric Functions Video Lesson Transcript Study Com



How Do You Find The Derivative Of Sin 1 2x 1 Socratic




Solve For X Tan 1 2x 1 X 2 Cot 1 1 X 2 2x Pi 3 1ltxlt1



Derivative Of Arctan X Inverse Tangent Detailed Lesson



How To Use The Excel Atan Function Exceljet




Solved Use Tan 1 Where 0 X 90 To Answer The Chegg Com



1




Derivatives Of Inverse Trigonometric Functions Sin 1 2x Cos 1 X 2 Tan 1 X 2 Sec 1 1 X 2 Youtube




Integration Of Tan Inverse X Ex 7 6 13 Chapter 7 Class 12




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube



Tan 2 Tan 1 X Tan 2 Arctan X Youtube



The Differential Coefficient Of Tan 1 2x 1 X 2 With Respect To Sin 1 2x 1 X 2 Is Sarthaks Econnect Largest Online Education Community



Let Tan 1 Y Tan 1 X Tan 1 2x 1 X 2 Where X 1 3 Then A Value Of Y Is Sarthaks Econnect Largest Online Education Community




Prove That Tan Inverse X Tan Inverse 2x 1 X Square Tan Inverse 3x X Cube 1 3x Square X Maths Inverse Trigonometric Functions Meritnation Com




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Tangent Half Angle Formula Wikipedia




Prove That Sin 1 2x 1 X 2 2sin 1x X 1 2




No Of Roots Of The Equation Tan Inverse 2x Tan Inverse 3x P 4 Brainly In




Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube




Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6




Solved Prove The Identity Cot 2x 1 Tan 2x 2 Tan X Chegg Com



Simplify The Trigonometric Expression Tan 2x Tan X Using Double Angle Identities A Brainly Com




Cos 2x Formula Derivation Examples What Is Cos 2a Formula




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube
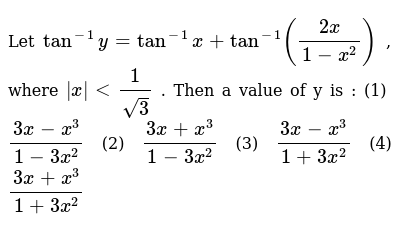



Let Tan 1 Y Tan 1 X Tan 1 2x 1 X 2 Where X 1 Sqrt 3 Then A Value Of Y Is 1 3x X 3 1 3x 2 2 3x X 3 1 3x 2 3 3x X 3 1 3x 2 4 3x X 3 1 3x 2



What Is The Value Of Tan 1 2 Cos Inverse 5 3 Quora




Weierstrass Substitution Wikipedia



Solve For X Tan 1 2x 1 X 2 Cot 1 1 X 2 2x P 3 1 X 1 Sarthaks Econnect Largest Online Education Community




Solve Tan 1 X Tan 1 2x 1 X 2 Pi 3




Example 13 Solve Tan 1 2x Tan 1 3x Pi 4 Class 12



1 Tan 2x Sec 2x




How To Solve Tan 1 2x 1 X2 Cot 1 1 X2 2x Pie 3 Brainly In
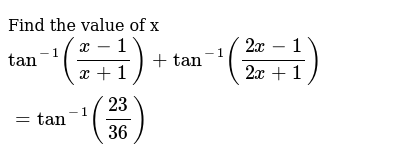



Find The Value Of X Tan 1 X 1 X 1 Tan 1 2x 1 2x 1 Tan 1 23 36




Example 13 Solve Tan 1 2x Tan 1 3x Pi 4 Class 12




Solved 1 A Show That The Function F X Y Given By Chegg Com




Solve Cos 1 X2 1 X2 1 Tan 1 2x X2 1 2pi 3 Brainly In




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Example 3 Show That Sin 1 2x 1 X 2 2 Sin 1 X Class 12



Power Series Of Arctan 2x Video Khan Academy




Weierstrass Substitution Wikipedia




What Are The Inverse Trigonometric Functions A Plus Topper Trigonometric Functions Math Formulas Studying Math




Properties Of A Inverse Trigonometric Function Tutorsonnet




Range Of Tan 1 2x 1 X 2 Is A Pi 4 Pi 4 B Pi 2 Pi 2 C Pi 2 Pi 4 D Pi 4 Pi 2




Ex 5 3 10 Find Dy Dx In Y Tan 1 3x X3 1 3x2 Ex 5 3
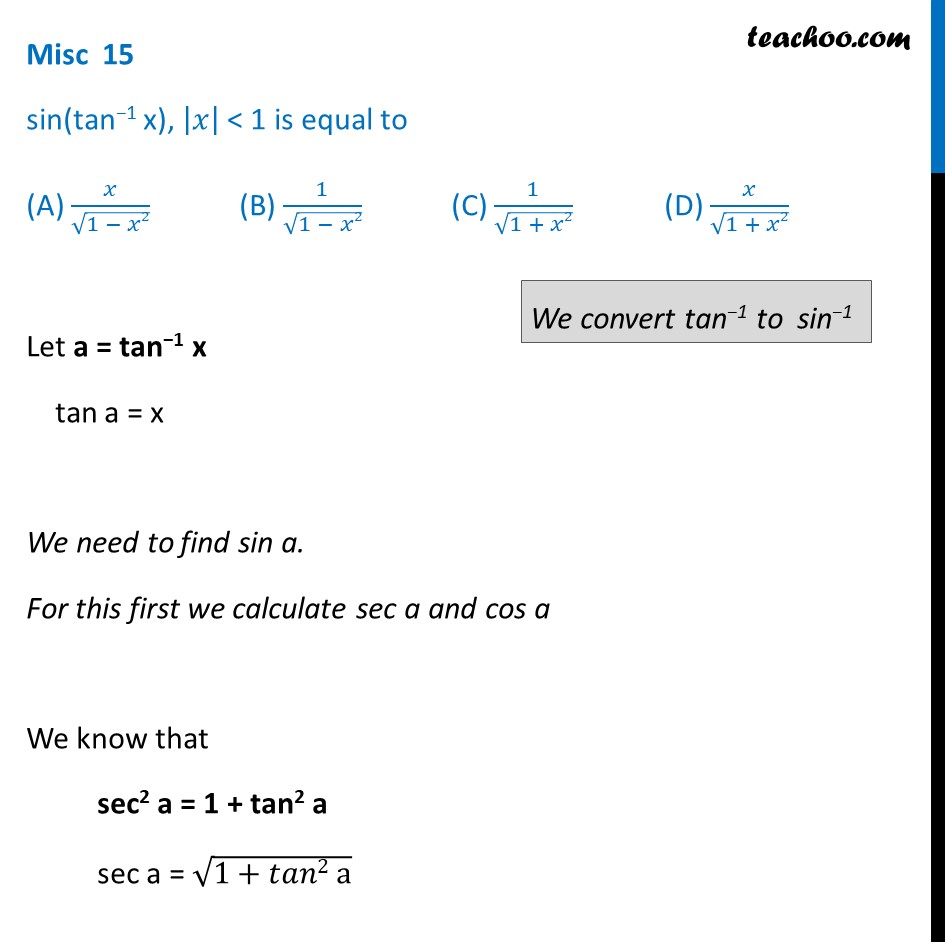



Solve Sin Tan 1 X Inverse Trigonometry Mcq Teachoo



Inverse Trigonometric Functions Precalculus Ii



What Is The Nth Derivative Of Tan 1 2x 1 X 2 Quora




Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6




Drill Find Dy Dx Y X 3 Sin 2x Y E 2x Ln 3x 1 Y Tan 1 2x Product Rule X 3 2cos 2x 3x 2 Sin



What Is The Formula Of Tan2x Quora




Solved Use Integration By Parts To Determine Which Of The Chegg Com




Example 13 Solve Tan 1 2x Tan 1 3x Pi 4 Class 12



Considering The Principal Solutions Find The Number Of Solutions Of Tan 1 2x Tan 1 3x Pie 4 Mathematics Topperlearning Com 7437




Find The Range Of Tan Inverse 2x 1 X 2




Tan2x 1 ただの悪魔の画像



What Is The Value Of Dy Dx If Y Tan 1 4 X 1 4x Quora




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube




Integration Of Inverse Tan 2x Integration By Parts Youtube




Solved Derive The Reduction Formula Prove The Reduction Chegg Com



What Is The Value Of Tan 1 Quora




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




How Do You Use Inverse Trigonometric Functions To Find The Solutions Of The Equation That Are In The Interval 0 2p Socratic



0 件のコメント:
コメントを投稿