無料ダウンロード ημ(π/2 θ) 240124-ημ(π/2+θ)

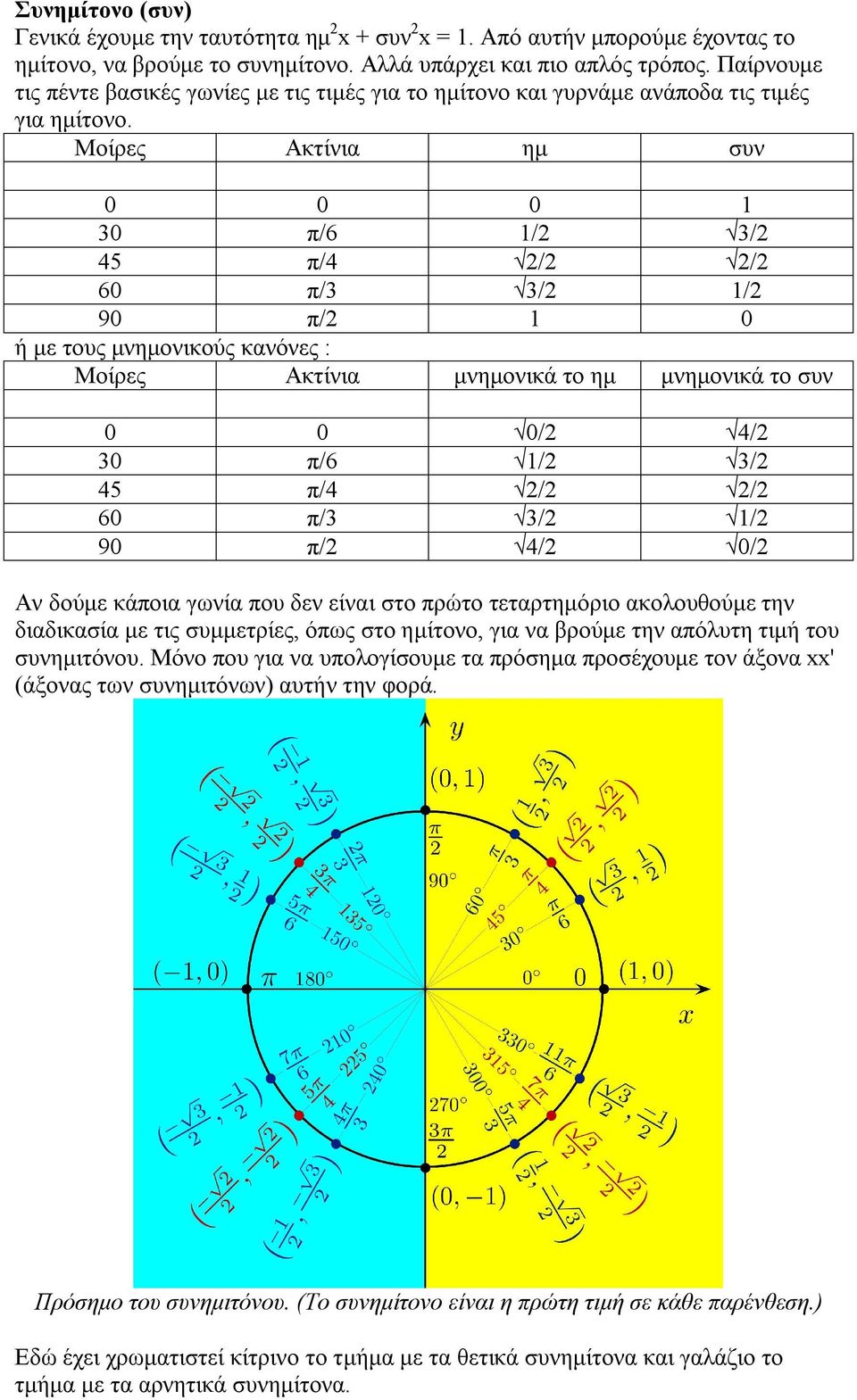
 Να αποδείξετε ότι έχει σταθερή τιμή ανεξάρτητη του θ η παράσταση π συν 2 (π θ) 2συν 2 ( θ) ημ(π θ)ημ(2π θ) 2 7 Γωνίες που διαφέρουν π/2 Γωνίες με άθροισμα π/2 Γωνίες αντίθετες ημ(θ)=ημθπ x 0, 2 α)Να λύσετε την εξίσωση f x 0 β)Αν θ η μεγαλύτερη ρίζα της προηγούμενης εξίσωσης, να αποδείξετε ότι 9π συν 2π θ εφ π θ συν θ 2 Α 1 17π ημ 11π θ συν θ σφ θ 2

1

ημ(π/2+θ)

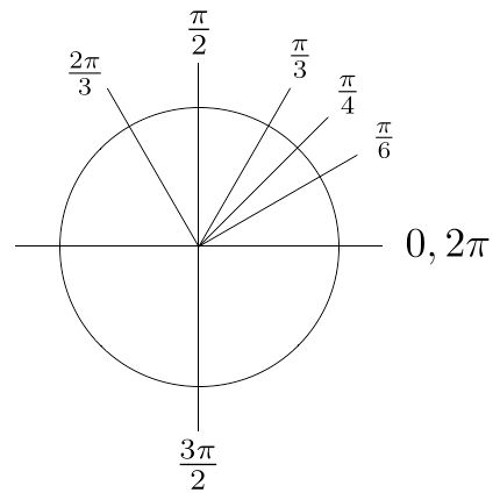
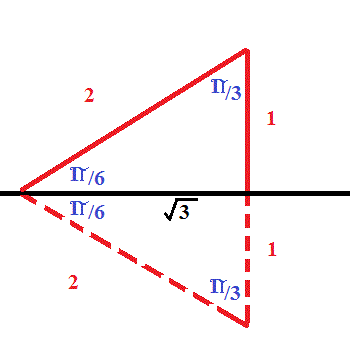
ημ(π/2+θ)-Να πολογσε rε ος ριγνομερικος αριθμος ης γνι yς θ ΒΓ 2 4 5 ημ =4 5 ΠΘ ( )2=( )( )2 52=( )2 42 25=( )2 16 ( )2 =25− 16=9 =√9 =30, π/6, π/4, π/3, π/2, , π 3 π/2, 2 π 1 Τόξα µε διαφορά π/2 ηµ ( π/2 θ) = συνθ εφ (π/2 θ) = σφθ συν (π/2 θ) = ηµθ σφ (π/2 θ) = εφθ 2 Τόξα µε διαφορά π

Academic Oup Com Mnras Article Pdf 504 4 6076 Stab311 Pdf

X=2κπθ ή x=2κππθ κ Αν 1π͙ʗ ημ225ο=ημͿ180ο45ο)= ημ45ο= √ /2 σφ240 ο =σφͿ180 ο 60 ο )= √ σφ60 ο = ΤΟΞΑ ΜΕ ΔΙΑΦΟΡΑ 2π ͘ φ ͖ 2πφ Ϳ1 ο ʐεʐαρ΀ ⇒ ημ ͖σʑν ͖εφ ͖σφ >02 36 π π Αν τώρα διαιρέσουμε τον 79 με τον 6 βρίσκουμε πηλίκο 13 και υπόλοιπο 1 Επομένως είναι 79 79 1 213 2132 36 6 3 ππ πππ , οπότε θα έχουμε 79 3 13 2 3332 πππ ημ ημ π ημ 79 1 332 ππ συν συν 79 3 33 ππ

The Trigonometric ratios of angle π/2θ Thinking of θ as an acute angle (that ends in the 1st Quadrant), (π/2 θ) or (90°θ) also ends in the 1st QuadrantSince in the 1st Quadrant, all trig ratios are positive;Therefore, all trig ratios of (π/2 θ) angle are also positiveWhat is the catch then?Note that if two angles add up to 90°, they are called " complimentary angles0 = π / 2 rad ͖ γιαʐί για t = 0 ͖ y = A ͙ Άρα ͘ F = – 10·0͖1·ημ ΁10·t Ϳπ / 2΀΂ ⇒ F = – 1·ημ ΁10·t Ϳπ / 2΀΂ ͿS͙I͙΀ ή F = – σʑν Ϳ10·t΀ ͙ ια να προσδιορίσοʑμε ʐην αλγεβρική ʐιμή ʐης Fελ

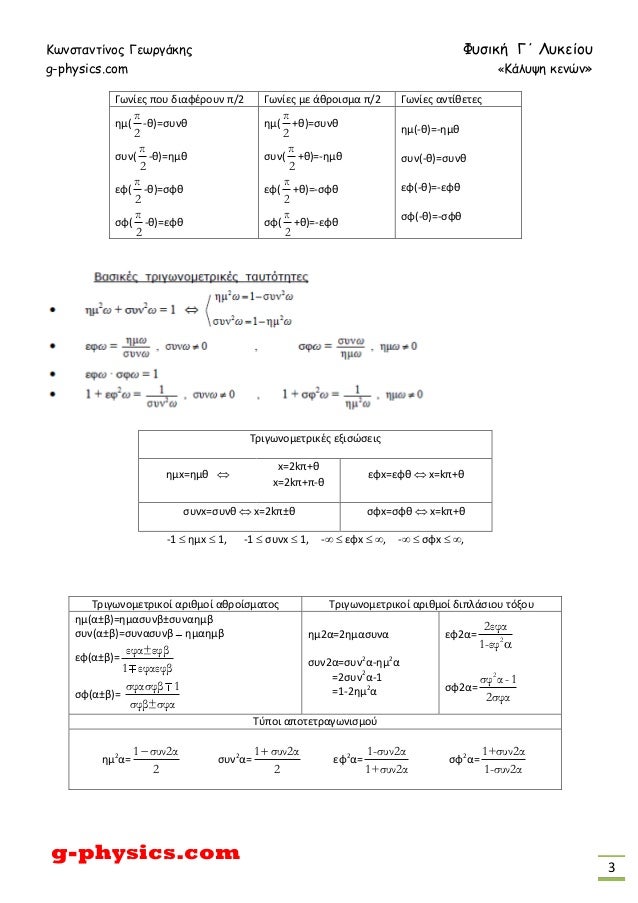
 01β_Γ' Λυκ Φυσ Προσ_Κενά Μαθηματικά 1 Κωνσταντίνος Γεωργάκης Φυσική Γ΄ Λυκείου gphysicscom «Κάλυψη κενών» gphysicscom 1 Απαραίτητες γνώσεις από την τριγωνομετρία Οι τριγωνομετρικοί αριθμοί οξείας γωνίας σε ορθογώνιο τρίγωνοπ 3) και στο (π 3, θ 2) με E΄(θ) = 2συν 2 θ συνθ – 1, θ∈(0, π) Οπότε, από ΘΜΤ, υπάρχει ξ 1 ∈(θ 1, π 3) τέτοιο ώστε Ε΄(ξ) = 1 1 π Ε( ) Ε(θ) 3 π θ 3 − − = 1 π3 Ε( ) 34 θ − − ⇔ (π 3 – θ 1)Ε΄(ξ 1) = Ε(π 3) 3 4 (i) ξ 2 ∈(θ 1, π 3 \Α^2 = (Α_1 Α_2 \cdot συνφ)^2 Α_2^2 \cdot ημ^2φ\ όπου \(φ = φ_{x2} φ_{x1}\) θετικός αριθμός Φροντίζουμε να αφαιρούμε από την φάση της ταλάντωσης που προηγείται την φάση της ταλάντωσης που έπεται

Projecteuclid Org Download Pdf 1 Euclid Ijm

The Beta Theta Pi Summer 16 By Beta Theta Pi Issuu

2 x ημ 3 x γ) −ημ ⋅ ημ 1 x 1 x 4 Απλοποιήστε τις κλασματικές παραστάσεις α) ημ x ηη x συν x συνx 4 2 4 2 β) συν x συνy x y 2 2 ημ ημ 2 2ΒυιμοΔαγμνάξ (θ θιάδμξ) ζηε π/ζ (ζέζε ΢μνεφηνα) ημο Δήμμο Κμηίμο Νειίμο ζοκέπεηα δοζμεκχκ θαηνηθχκ ζοκζεθχκ πμο επηθναημφκ ζηε πενημπή (πημκυπηςζε) απυ ζήμενα απυ ημ 2 μ 17μ πιμ2 98 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ • Ο πολλαπλασιασμός του μιγαδικού z = 1 1 ( ρ θ 1 i συν ημ θ 1) με το μιγαδικό z = 2 2 ( ρ θ 2 i συν ημ θ 2) σημαίνει στροφή της διανυσματικής ακτίνας του κατά

2

Etd Ohiolink Edu Apexprod Rws Etd Send File Send Accession Case Disposition Inline

Τ 2/3 7 ζ Π 2/4 6 στ Κ 2/5 Πάσχα 3 γ Τ 2/6 12 ιβ Π 2/7 8 η Δ 2/8 17 ιζ Δ Π Σ Τ Π Κ ΗΜ/ΝΙΑ ΗΜ/ΝΙΑ ΗΜ/ΝΙΑ ΗΜ/ΝΙΑ ΗΜ/ΝΙΑ ΗΜ/ΝΙΑ 14/9 16 ιστ 14/10 ΠΡΑΞ 1 α 14/11 4 δ 14/12 2 β 14/1 4 δ 14/2 9 θ Φύλλο 27 Κ Τ Π ΔΠ χ αν έχουμε τις ταυτότητες για τα αντίθετα και τα διαφέροντα κατά π/2 τόξα, που αποδείχτηκαν παραπάνω εύκολα και με πληρότητα, δηλ αν έχουμε τις ταυτότητες συν(–θ)=συνθ, ημ(–θ)=–ημθ, συν(π/2υ = υmaxημ(ωt π/2) ημθ = ημ(πθ) , συνθ = ημ(π/2θ) α = αmax ημ(ωt π) Δηλαδή η ταχύτητα προηγείται της απομάκρυνσης κατά π/2 και η επιτάχυνση της ταχύτητας κατά π/2 και της απομάκρυνσης κατά π

Optimal Insurance Package And Investment Problem For An Insurer

Q Tbn And9gcrvvb6gqg0xx4owdkrcvprmdee2rkcyqgsrns5n8ck6jizpc6va Usqp Cau

 ΤΥΠΟΛΟΓΙΟ ΦΥΣΙΚΗΣ by mt tsilp issuu Τυπολόγιο Φυσικής 60 Παράρτημα Α Τριγωνομετρικοί Τύποι απέναντι κάθετος2 2( ) x κπ θ x κπ π ημ2x = ημ(xπ 2) ε) εφ3x=εφx 2 Να λύσετε τις εξισώσεις α) ημx = συνx β) ημ2x = ημ(xτου π/2 τότε οι τριγωνομετρικοί αριθμοί εναλλάσσονται (ημ με συν και εφ με σφ) Για να βρούμε το πρόσημο, διαιρούμε τον αριθμητή του κλάσματος, που μας δίνεται, με το 4

Stream P 2 Radians By The Illuminator Listen Online For Free On Soundcloud

Optimizing The Decoy State 84 Qkd Protocol Parameters Springerlink

Πχ αν ο Οχ' διαγράψει 2 πλήρεις στροφές και στη συνεχεία γωνία 40ο, τότε έχει διαγράψει γωνία ω= ⋅ =2 360 40 7600 0 0 Αν ο θετικός ημιάξονας Οχ κινούμενος κατά την αρνητική φορά( με τη φορά της κίνησης τωνΟπότε Δℓ = 0,2 0,2 ∙ημ (10 ∙t 3π/2) SI Για t ≥ t1 → x = A∙ημ ω(t–t1) θ → 4 π Δl 0,2 2 ημ 10 t 0,05 π SI Τ/4 Τ/2 3Τ/4 Τ (t 1) (t 2) t Δℓ (m) 0,2 2 0,2 T = 0,2 π sec 0,2 2 0 ΘΙ (β) → ΘΙ (α) → θ (t1) A (t2) ωΔ t x1 Υπάρχει γωνία ω με ημω=0 και συνω=0 2 Η μεγαλύτερη τιμή της παράστασης Α=3ημx είναι 3 3 Η εφω δεν ορίζεται όταν ω= , 2 4 Μια γωνία 750 είναι ίση με 5 12 5 εφ (x)εφx=0 6 συν ( x ) x 2 7 ημ1050=συν150 8 Είναι συν (πω

01b G Lyk Fys Pros Kena Ma8hmatika

The Associative Structure Of The Copper Plaques Chapter 2 The Textualization Of The Greek Alphabet

π = ημ 2 3 π ζ) ημ3x = ημ 2 π θ) Η εξίσωση ημπx = 0 , έχει λύσεις όλους τους ακέραιους αριθμούς ι) Ισχύει ότι συνπx = 0 ⇔ Ένα λιβάδι με ήλιους Μια άσκηση που δεν δημιουργήσαμε εμείς Επιστρέψτε στη σελίδα Ασκήσεις στη φυσική της Γ΄ λυκείου Δείτε και αυτό Σύνθεση απλών αρμονικών ταλαντώσεων ΙΙΙ Ένα σώμα μάζας m = 0,4 kg , εκτελεί ταυτόχρονα2ιστ ισχύει ημ 50ο ο ημ240 = 1 ιζ ισχύει ημ 270 ο ημ = 1 ιη ισχύει συν280 ο συν2170 = 1 Β) Ερωτήσεις πολλαπλής επιλογής i οΤο μέτρο της γωνίας θ = 40 σε rad είναι Α π 5 Β 3π 4 Γ 2π 9 Δ π 12 Ε 3 ii Το μέτρο της

Arxiv Org Pdf 1905 1

Tipologio By Mathkostas Issuu

MULTIPLICATIONS ON HOMOGENEOUS SPACES 249 L(G) = {L(d)aeG} and s{μ, X) is the usual left invariant vector field generated by X, so our results are consistent with Lie theory In the case of a Γ invariant multiplication μ, we obtain the connection induced by μ is given by the algebra (m, a) with α(X, Y) = F\Θ)(X, 0), (0, Y)\ = 1J2XQY where Q is the endomorphism of m given byUse the fact that θ is a constant when computing limits as h goes to 0 The limit \lim_ {\theta \to 0}\frac {\sin (\theta )} {\theta } is 1 The limit lim θ → 0 θ s i n ( θ) is 1 To evaluate the limit \lim_ {h\to 0}\frac {\cos (h)1} {h}, first multiply the numerator and denominator by \cos (h)1 To evaluate the limit lim h → 0 h c oΠαράδειγμαΝαλύσετετιςεξισώσεις α) 3 εφx 3 β)σφx 1 0 Λύση α) 3 π π εφx ημx ημ x κπ 3 6 6 με κ Ζ β)

2

3

Πανελλήνιο Σχολικό Δίκτυο Το Δίκτυο στην Υπηρεσία της Εκπαίδευσης3 Να σημειώσετε την σωστή απάντηση σε κάθε μια από τις επόμενες ερωτήσεις α) Η εφ( 30ο) είναι ίση με Α εφ60ο Β σφ60ο Γ σφ30ο Δ εφ30ο β) Το συν0ο είναι ίσο με Α συν ο Β Γ ημο Δ συνοH επιτάχυνση προηγείται της ταχύτητας κατά π/2 rad και της απομάκρυνσης κατά π rad Άρα υ=0,4π·ημ 2tπ και x=0,2·ημ π 2t 2 π− (SI) γ Η ταχύτητα είναι μηδέν στις ακραίες θέσεις στις οποίες είναι α max

Arxiv 2102 v2 Math Oc 16 Feb 21

Psyarxiv Com Ebym7 Download Format Pdf

1) Ένα κινη ό εκ ελεί σγχρόνως δύο απλές αρμονικές αλαν ώσεις πο γίνον αι σην ίδια διεύθνση και γύρω από ην θέση ισορροπίας με εξισώσεις x 1 = 3·ημ (2·π)·t και x 2 = 4·ημ (2·π)·t φ , (SI) Να βρείε ην εξίσωση ης απομάκρνσης x (t Check Pages 1 6 of Τριγωνομετρία in the flip PDF version Τριγωνομετρία was published by x_tsak on Find more similar flip PDFs like Τριγωνομετρία Download Τριγωνομετρία PDF for freeX2κπ θ ημx α,κ x2κπ π θ Αξονας συνημιτονων Α ξ η μ ι τ ο ν ω ν πθ α θ θ θ πθ θ 1 111 0 π/2 π 3π/2 2π Ομοιοτρόπως αν το α αρνητικός και μεγαλύτερος του 1 1 Παράδειγμα

2

Trigwnometria Giwrgos Karipidhs 2 An8oyla Sofianopoyloy Pdf Free Download

α) εφ(3πω)∙σφ(4πω) συν 2 7πω ημ 2 (5πω) β) εφ πφ ∙συν(2πφ)∙συν( 9π 2 φ) ημ(13πφ)∙συν(φ)∙σφ( 21π 2 φ)322Έστω εφθ = με π < θ < π Να υπολογισθούν οι υπόλοιποι τριγωνομετρικοί αριθμοί της γωνίας θ ΛΥΣΗ ⇒ σφθ = εφθ ⇒ σφθ = ˇ ˆ˙ ⇒ σφθ = Όμως ημ θ συν θ = 1 ⇒ ημ θ συν θ συν θ συν θ = συν θ ⇒ εφ θ 1 = συν θΚατά την μέτρηση σε ακτίνια, μια γωνία θ ακτινίων θα αντιστοιχεί σε ένα τόξο, του οποίου το μήκος είναι rθ, όπου r είναι η ακτίνα του κύκλου ( 0 ≤ y < π/2 ή π/2 <

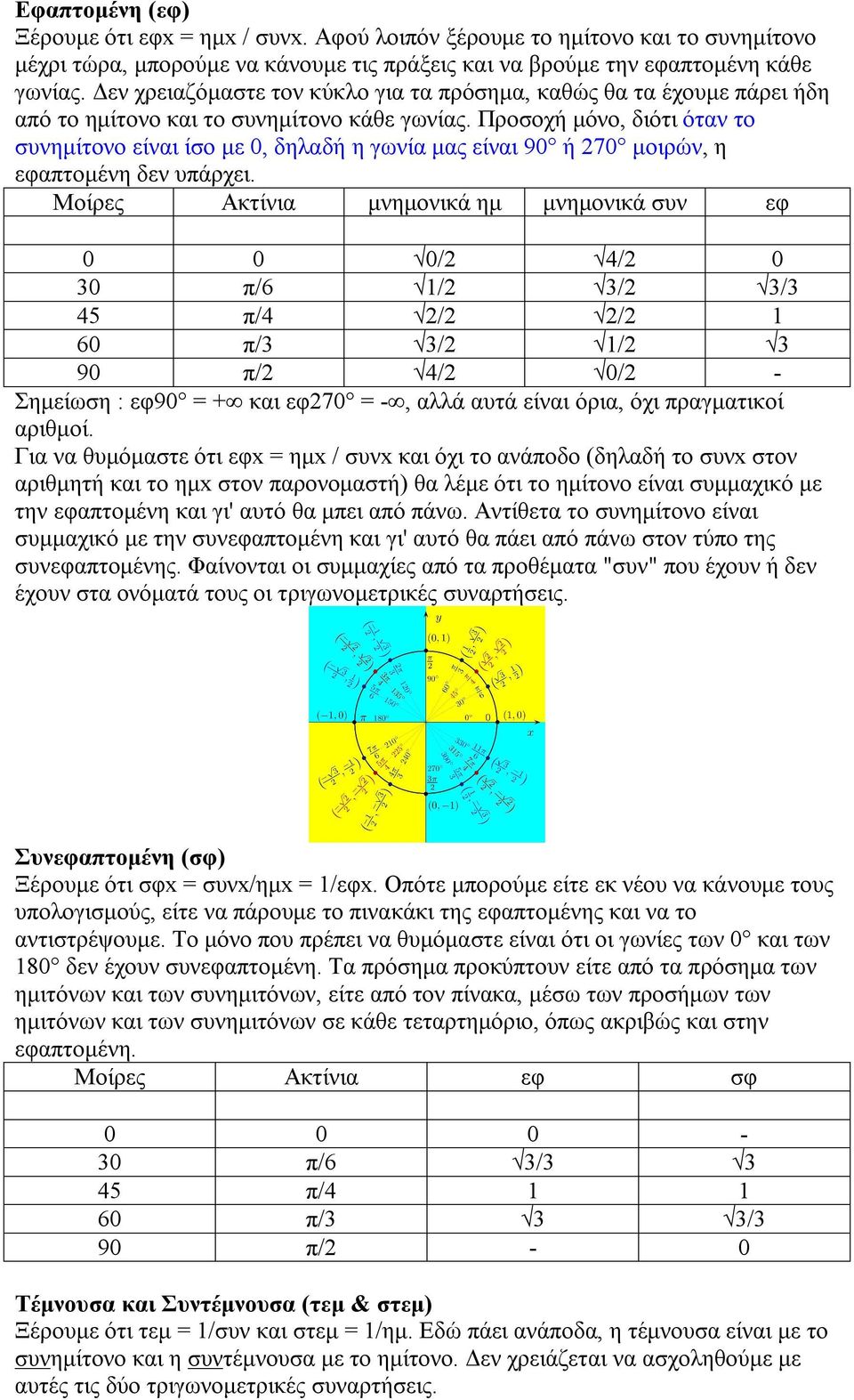
P 6 45 P 4 60 P 3 90 P 2 Pdf Free Download

Generalized Linear Model An Overview Sciencedirect Topics

 Check Pages 1 50 of ΑΛΓΕΒΡΑ Β΄ΛΥΚΕΙΟΥ ΒΙΒΛΙΟΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣ in the flip PDF version ΑΛΓΕΒΡΑ Β΄ΛΥΚΕΙΟΥ ΒΙΒΛΙΟΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣ was published by Arnos Online Education on Find more similar flip PDFs like ΑΛΓΕΒΡΑ Β΄ΛΥΚΕΙΟΥ ΒΙΒΛΙΟΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣSince our angle is greater than π and less than or equal to 3π/2 radians, it is located in Quadrant III In the third quadrant, the values for tan are positive only Determine angle type 225 is an obtuse angle since it is greater than 90° sin(5π/4) = √ 2 /2 Multiply our answer by our coefficient of 5 5sin(5π/4) = 5(√ 2 /2)ο,2 π φ = 2 Άρα η εξίσωση απομάκρυνσης του Σ2 είναι 2 π x = 0,1 ημ 10t (SI) 2 ε) Ο ρυθμός μεταβολής της ορμής του Σ1 είναι 1 2 1 1 1 1 o,1 Δp 3π = ΣF = Dx = m ω A ημ ωtφ = 30ημ 10t (SI) Δt 2

2

Plasma Physics Home Page For Richard Fitzpatrick The University

The House Of E T A Dance Photos Facebook

Www Scielo Br J Rbef A 6kqff8szfxdrvcgxt8hs6hk Lang En Format Pdf

Www Ntnu Edu Documents Phd Thesis Caharija Pdf F3a1bda7 2108 4f6a 9949 6cbd457f16db

Pubs Acs Org Doi Pdf 10 1021 Acs Langmuir 7b Src Recsys

When Will Maths Move On Like The Church Did And Stop Giving The Sermon In Latin Greek Letters Etc And Teach The Subject In English The Concepts Are Not That Difficult But

Iopscience Iop Org Article 10 10 1555 6611 Ab31 Pdf

Www Nature Com Articles S 021 X Pdf Origin Ppub

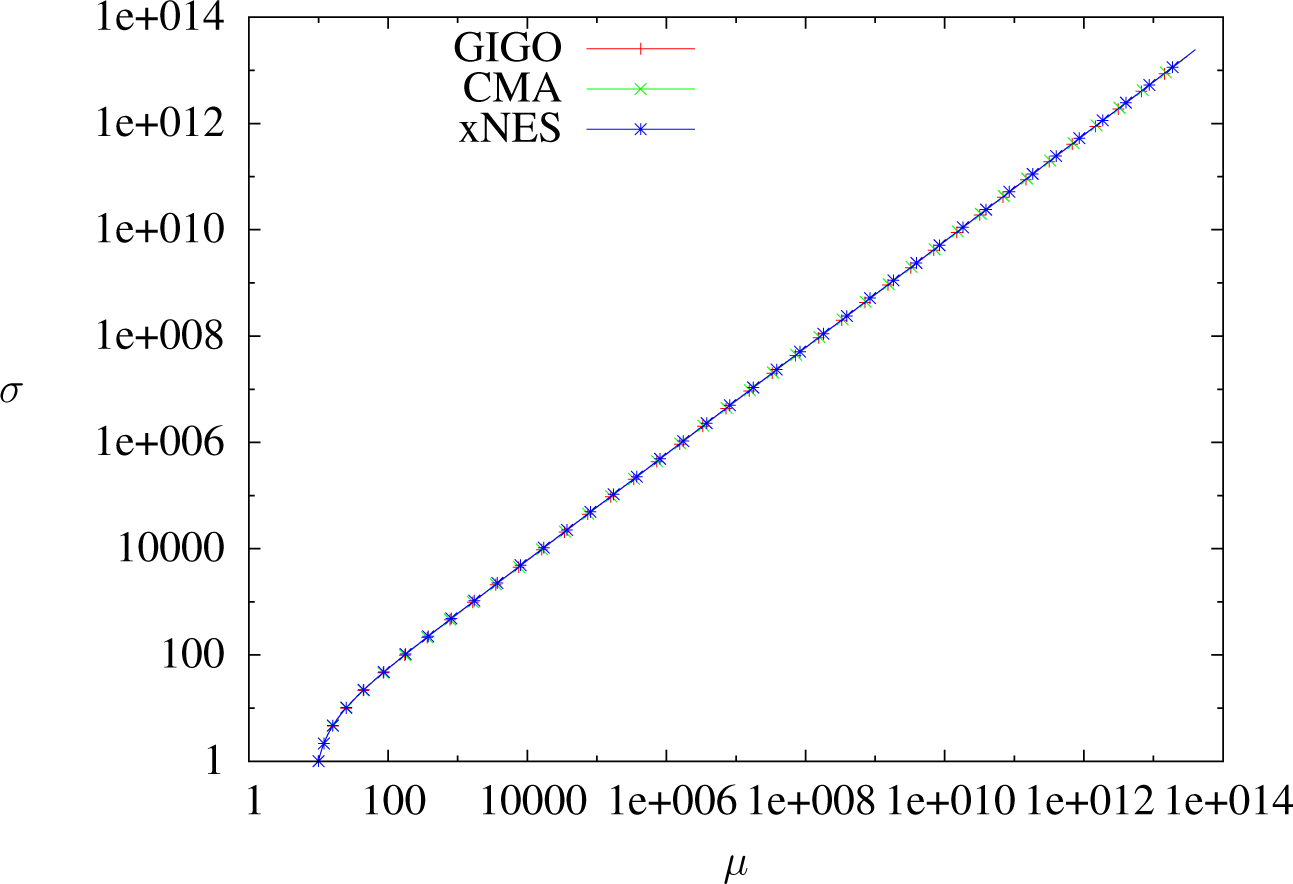
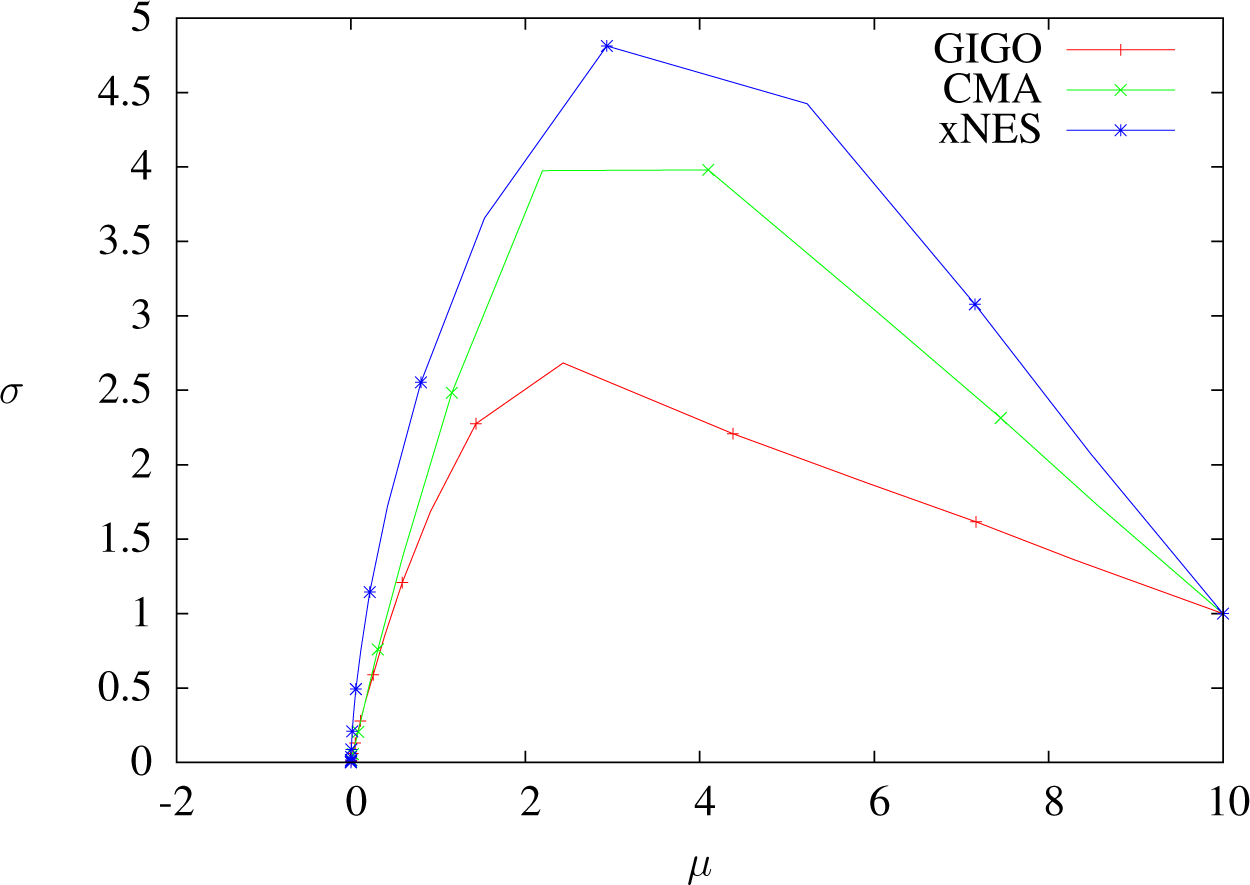
Entropy Free Full Text Black Box Optimization Using Geodesics In Statistical Manifolds Html

2

Entropy Free Full Text Black Box Optimization Using Geodesics In Statistical Manifolds Html

2

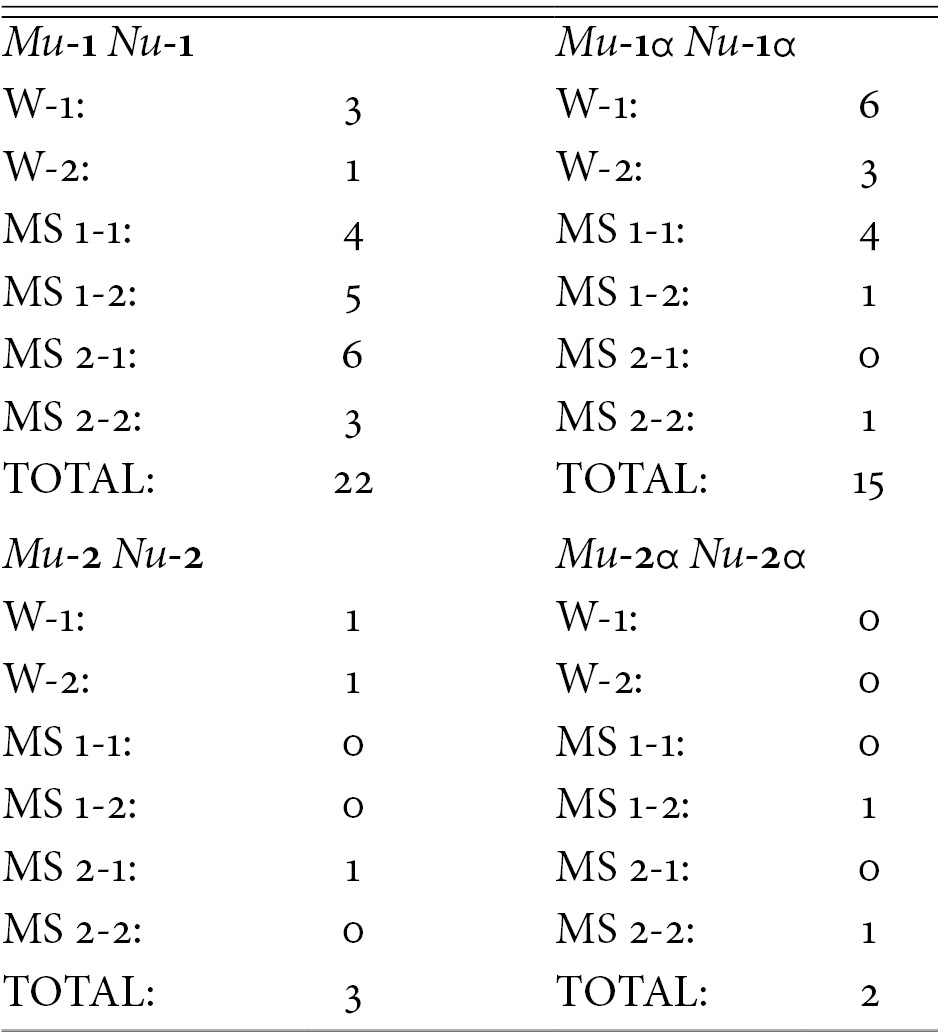
The Associative Structure Of The Copper Plaques Chapter 2 The Textualization Of The Greek Alphabet

Generalized Linear Model An Overview Sciencedirect Topics

Shifting Angle By P 2 P 3p 2 2p Finding Value Of Trignometric F

Http Users Sch Gr Gkaripid Theory B lik Trigonometry1 Pdf

Http Moriond In2p3 Fr Download Proceedings Moriond Ew 19 Pdf Pdf

Lymenes Askhseis Trigwnometria 1 Na Breite Toys Ari8moys I Hm Ii Syn Lysh I Diairwntas To 1125 Me To 360 Briskw Pdf

1

2

How Do You Evaluate Sin 11p 6 Socratic

Pdf Local Development Of Settlements In The Municipality Of Konitsa Epirus Region Topikh Anapty3h Twn Oikismwn Toy Dhmoy Konitsas Perifereias Hpeiroy Dimitris P Drakoulis And Vagelis Dimitriadis Academia Edu

2

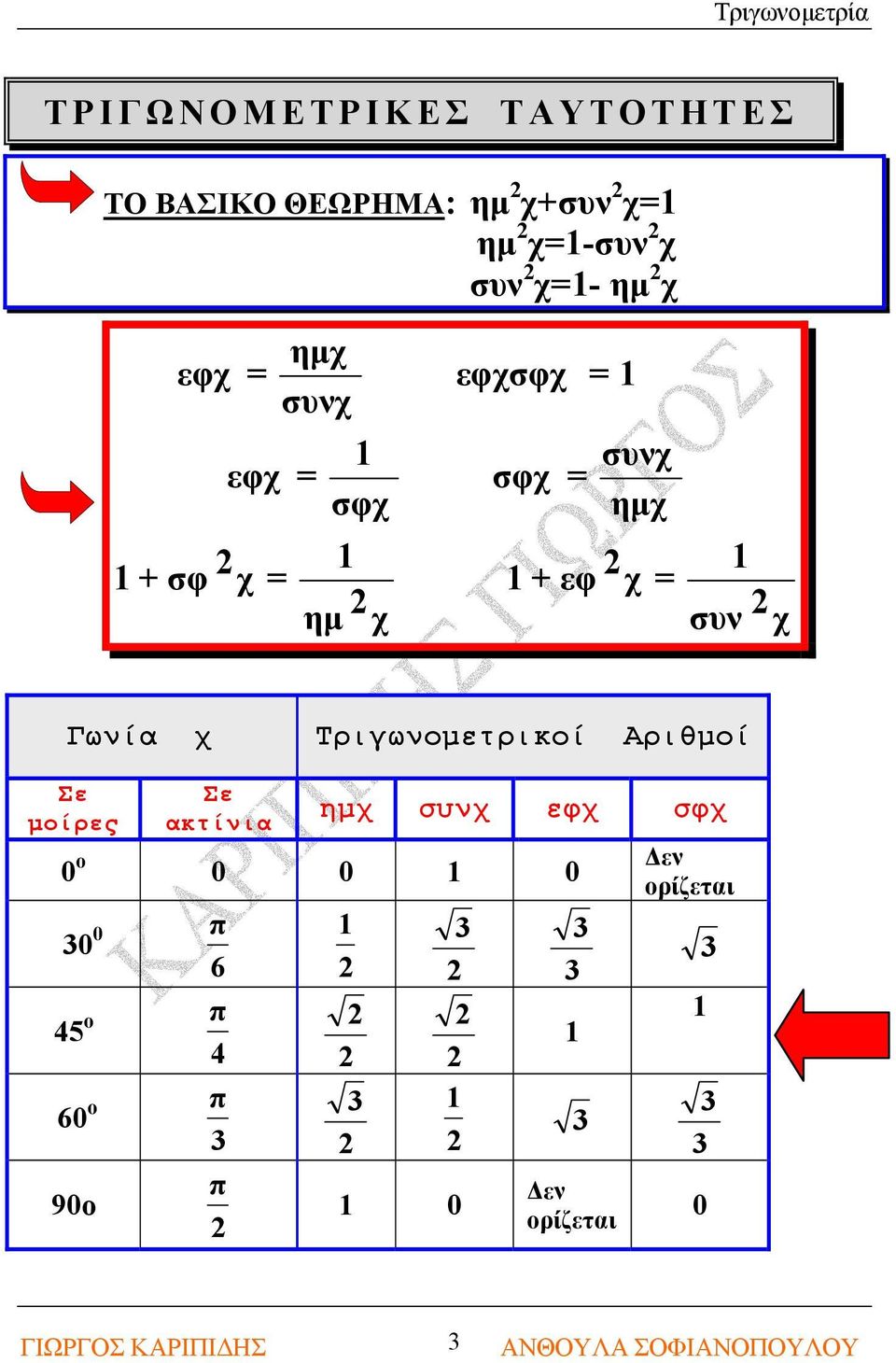
Trigwnometria Giwrgos Karipidhs 2 An8oyla Sofianopoyloy Pdf Free Download

Lymenes Askhseis Trigwnometria 1 Na Breite Toys Ari8moys I Hm Ii Syn Lysh I Diairwntas To 1125 Me To 360 Briskw Pdf

2

Trigwnometria Pages 1 6 Flip Pdf Download Fliphtml5

Blue White And Red Ocean Planets Simulations Of Orbital Variations In Flux And Polarization Colors Astronomy Astrophysics A A

Tipologio By Mathkostas Issuu

Http Www Askisopolis Gr Upload 3790 23 Ce Cf 81 Ce B9 Ce Cf Ce Ce Bf Ce Ce B5 Cf 84 Cf 81 Ce Af Ce B1 Pdf

Http Xhmeia Weebly Com Uploads 9 5 9 6 1 Pdfsam 111sp Pdf

Find The Exact Value Of Sin Pi 12 Youtube

Design Of M Channel Linear Phase Non Uniform Filter Banks With Arbitrary Rational Sampling Factors Fang 16 Iet Signal Processing Wiley Online Library

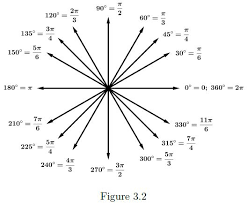
How Do I Find The Value Of Sin 5pi 6 Socratic

Bodleian Digital Library Systems And Services The Chch Oxford Copy Of John Fell S Specimen Of Type Which Was Bequeathed To Oxford University Press After His Death T Co Swiuy0ngra T Co Quf2dyhl38

Academic Oup Com Mnras Article Pdf 504 4 6076 Stab311 Pdf

Manuscripts In St Catherine S Monastery Mount Sinai Available Online Greek Manuscripts 592 Menaion Dec Feb Amedmonastery a Ms Available Online Library Of Congress

Turbomole User S Manual Manualzz

Clarkson R Mckeon D G C Quantum Field Theory U Waterloo Quantum Field Theory Docsity

The Associative Structure Of The Copper Plaques Chapter 2 The Textualization Of The Greek Alphabet

1

The M Bar K 0 Mu Distributions Of The A D Rightarrow Download Scientific Diagram

Transition Among States N 4 N 0 2 M 1 M 2 1 And K 7 Download Scientific Diagram

Plain Double Letter Guard J Brandt Recognition

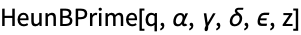
Heunb Wolfram Language Documentation

Osa Fringe Pattern Analysis Using A 2 D Fourier Transform

Http Www Physics Mcgill Ca Cumming Teaching 352 Phys352 All Notes Pdf

Osa Fringe Pattern Analysis Using A 2 D Fourier Transform

Econ Pku Edu Cn Docs 12 Pdf

Xanthippi Papadopoulou Poweroflovegr Prin 4 omades Sxolio Toy Isaak Ston Kyriako Pozeroy Sthmenooooo

Http 7lyk N Smyrn Att Sch Gr Joomla Test Attachments Article 198 Ce 92 Ce 9b Cf 85 Ce Ba Ce B5 Ce Af Ce Bf Cf 85 Ce 86 Ce Ce Ce B5 Ce B2 Cf 81 Ce B1 31 Ce Cf 81 Ce B9 Ce Cf Ce Ce Bf Ce Ce B5 Cf 84 Cf 81 Ce Af Ce B1 Pdf

Kef 3o Trigwnometria

Kef 3o Trigwnometria

Solutions Manual Signals And Systems 2nd Ed Haykin

Church Fathers Dev Gregorynazianzus 19 Xml At Master Opengreekandlatin Church Fathers Dev Github

How Do You Evaluate Sin 2 Pi 6 Socratic

Image 91 Of Greek Manuscripts 592 Menaion Dec Feb Library Of Congress

Psyarxiv Com Ebym7 Download Format Pdf

The Moser Tardos Framework With Partial Resampling

Ocr Results For Proclus 1618 In Platonis Theologiam Libri Sex

Proof Of Sin P 2 8 Cos8 Upto Cosec P 2 8 Sec8 Using Euler S Formula Youtube

2

Trigwnometria 8ewria Me8odologia Toy Dhmhtrh Mosxopoyloy

On Sinc Discretization And Banded Preconditioning For Linear Third Order Ordinary Differential Equations Bai 11 Numerical Linear Algebra With Applications Wiley Online Library

A Chemist S Guide To Density Functional Theory Institute For

Hard Limits And Performance Tradeoffs In A Class Of Sequestration Feedback Systems Biorxiv

Academic Oup Com Mnras Article Pdf 385 4 80 Mnras0385 80 Pdf

Talk Petanque Greece Photos Facebook

Ocr Results For Zonaras Joannes 1808 Lexicon

Arxiv Org Pdf 1905 1

Link Aps Org Pdf 10 1103 Physrevd

2

P 6 45 P 4 60 P 3 90 P 2 Pdf Free Download

Http Cds Cern Ch Record 7410 Files Cern 06 009 Pdf

Modified Gravity Without Dark Matter Arxiv Vanity

2

Distributions Of Cos 8 W E Upper The Cosine Of The Angle Between The Download Scientific Diagram

Hard Limits And Performance Tradeoffs In A Class Of Sequestration Feedback Systems Biorxiv

3 5 Basikes Trigwnometrikes iswseis

Arxiv Org Pdf 2107 064

2

2

Ir Stonybrook Edu Xmlui Bitstream Handle Atnv66i2final Pdf Sequence 2

Incoming Term: ημ(π/2+θ),